Chapter 5d - Pumping Loss Simple Analysis

Throughout this analysis we have assumed that at any instant the pressure is constant throughout the engine. However we find that the high heat fluxes required in the heat exchangers in turn requires a large wall/gas, or wetted area Awg. This requirement together with the conflicting requirement of a low void volume will result in heat exchangers with many small diameter passages in parallel. The fluid friction associated with the flow through the heat exchangers will in fact result in a pressure drop across all the heat exchangers which has the effect of reducing the power output of the engine. This is referred to as the "Pumping Loss" and in this section we attempt to quantify this power loss. We first evaluate the pressure drop across all three heat exchangers with respect to the compression space. Subsequently we can determine the new value of work done by integrating over the complete cycle, and isolate the Pumping Loss term as follows:

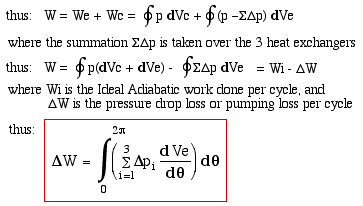
The pressure drop Δp is due to fluid friction as it flows through the heat exchanger sections. Our model has assumed one-dimensional flow throughout, however the fundamental concepts of fluid friction paradoxically break down under one-dimensional flow. Newton's law of viscosity states that the shear stress τ between adjacent layers of fluid is proportional to the velocity gradient ( d u/ d z) in these layers normal to the flow direction, as shown:

From the equation we see that a Newtonian fluid cannot sustain a shear stress unless the flow is two dimensional. This paradox is bypassed by stating that the flow is not strictly one-dimensional, but rather represented by its mean bulk mass flow rate. The dynamic viscosity μ is basically a measure of the internal friction which occurs when the molecules of the fluid in one layer collide with molecules in adjacent layers travelling at different speeds, and in so doing transfer their momentum.

Over the pressure range of interest the dynamic viscosity μ is independent of pressure. Its temperature dependence for the gasses of interest is obtained as in the diagram below (Refer: Bretsznajder, A, 1971, "Prediction of the transport and Other Physical Properties of Fluids", International Series of Monographs in Chemical Engineering, II, Oxford: Pergamon)

The frictional drag force F is related to the shear stress τ as follows:

F = τ Awg

where Awg is the wall/gas, or wetted area of the heat exchanger.

In setting up the working expressions to describe pumping loss we introduce the concept of a "hydraulic diameter" d, which describes the ratio of the two important variables of a heat exchanger - the void volume V and the wetted area Awg:

d = 4 V / Awg

The factor 4 is included for convenience. For flow in a circular pipe ( or a homogeneous bundle of circular pipes) the hydraulic diameter thus becomes equal to the pipe internal diameter. Substituting in the force equation above:

F = 4 τ V / d

We now define a Coefficient of Friction Cf as the ratio of the shear stress τ to the "dynamic head" (Refer to " Compact Heat Exchangers ", Kays & London):

where ρ is the fluid density and u is the fluid bulk velocity. Thus substituting for τ in the force equation we obtain the frictional drag force in terms of the Coefficient of Friction:

Under the quasi-steady flow assumption (no acceleration or deceleration forces) the frictional drag force is equal and opposite to the pressure drop force, thus:

F + Δp A = 0

where A is the cross sectional (free flow) area. Substituting for F, the pressure drop Δp is given by:

Note that Δp can be positive or negative, depending on the direction of flow. However the second term in this equation is always positive, and thus the equation violates the momentum conservation principle in the case of reversing flow. We resolve this by defining a "Reynolds Friction Coefficient" (Cref) by multiplying the Reynolds Number by the Coefficient of Friction as follows:

Cref = Nre Cf

Where Nre = ρ u d / μ is the Reynolds Number, defined and discussed in the section Scaling Parameters . By definition, the Reynolds Number is always positive, independant of the direction of flow. Thus finally:

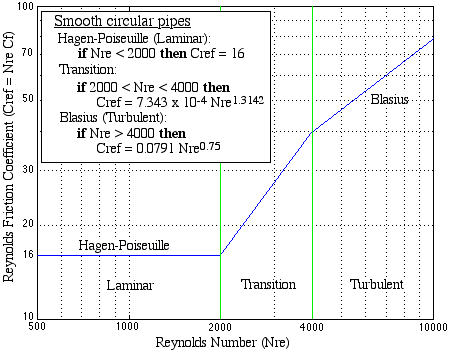
This equation satisfies the momentum conservation principle for both positive and reversed flow, since the sign of Δp is always correctly related to the sign of the velocity u. Since all current empirical data on the Coefficient of Friction is presented as a function of Reynolds Number, it is a simple matter to convert that data to the required Reynolds Friction Coefficient. For example, the Coefficient of Friction vs Nre curves for circular pipes (Moody Diagram) have been in widespread use over the past half a century. These curves have been simplified and rearranged in terms of the Reynolds Friction Coefficient Cref as follows:

Similar formulations can be done for the various heat exchanger and regenerator types of interest. (Refer to " Compact Heat Exchangers ", Kays & London).

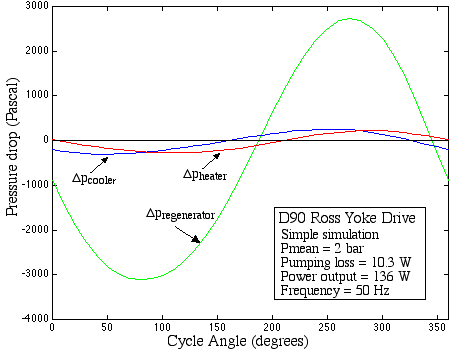
The Simple simulation of our D90 Ross Yoke-drive engine case study results in the following pressure vs crankangle plots. The first plot shows the pressure drop across the three heat exchangers. Note the relative magnitude (as well as the phase) of the regenerator pressure drop with respect to those of the heater and cooler.

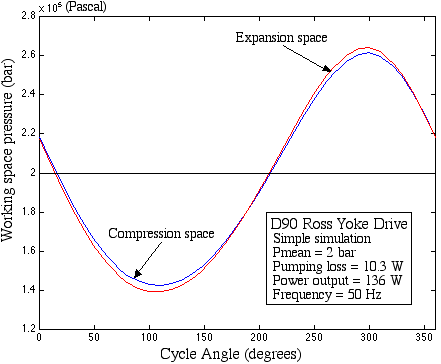
The following plot shows the expansion and compression space pressures vs crankangle. Under these conditions the pumping loss is 10.3 W, or about 7.5% of the net output power.

The complete simulation package including the pressure drop (pumping) loss, heat transfer and regenerator loss is described in the following section "Function set ' simple ' ".

Stirling Cycle Machine Analysis by Israel Urieli is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License