Course Web Page

    Course: MATH 3050

    Title: Discrete Mathematics

    Section: 101 (Class Number 6353)

    Campus: Ohio University, Athens Campus

    Department: Mathematics

    Academic Year: 2018 - 2019

    Term: Spring Semester

    Instructor: Mark Barsamian

    Contact Information: My contact information is posted on my web page .

    Office Hours for 2018 - 2019 Spring Semester: 9am - 10am Mon - Fri in Morton 538

    Course Description: Course in discrete mathematical structures and their applications with an introduction to methods of proofs. The main topics are introductions to logic and elementary set theory, basic number theory, induction and recursion, counting techniques, graph theory and algorithms. Applications may include discrete and network optimization, discrete probability and algorithmic efficiency.

    Prerequisites: C or better in MATH 2301 or MATH 263B and WARNING: No credit for both this course and CS 3000 (first course taken deducted)

    Special Needs: If you have physical, psychiatric, or learning disabilities that require accommodations, please let me know as soon as possible so that your needs may be appropriately met.

    Meeting Times and Locations: Section 101 (Class Number 6353), taught by Mark Barsamian, meets Mon, Wed, Fri 10:45am - 11:40am in Morton Hall Room 122

    Syllabus: This web page replaces the usual paper syllabus. If you need a paper syllabus (now or in the future), unhide the next two portions of hidden content (Textbook, Calendar) and then print this web page.

    Textbook Information:

    Textbook Information for 2018 - 2019 Spring Semester MATH 3050

    Title: Discrete Mathematics with Applications, 4 th Edition

    Author: Suzanna Epp

    Publisher: Brooks/Cole (Cengage Learning), 2010

    ISBN-10: 0495391328

    ISBN-13: 978-0495391326

    The book is widely-available at a huge range of prices. Save money by getting a used copy. (And note that we are not using the most recent edition of the text. This should help make used copies quite cheap.)

    Calendar:

    Calendar for 2018 - 2019 Spring Semester MATH 3050 Section 101 taught by Mark Barsamian

    Week 1: Mon Jan 14 - Fri Jan 18

    Week 2: Mon Jan 21 - Fri Jan 25

    Week 3: Mon Jan 28 - Fri Feb 1

    Week 4: Mon Feb 4 - Fri Feb 8

    • Day #8: Section 5.3 Mathematical Induction II
    • Day #9: Section 5.6 Defining Sequences Recursively (Quiz 3)
    • Day #10: Section 5.7 Solving Recurrence Relations by Iteration

    Week 5: Mon Feb 11 - Fri Feb 15

    • Day #11: In-Class Exam 1 on Chapters 4 and 5
    • Day #12: Section 9.1 Introduction to Counting and Probability
    • Day #13: Section 9.2 Possibility Trees and the Multiplication Rule

    Week 6: Mon Feb 18 - Fri Feb 22

    • Day #14: Section 9.3 Counting Elements of Disjoint Sets: The Addition Rule (Quiz 4)
    • Day #15: Section 9.5 Counting Subsets of a Set: Combinations
    • Day #16: Section 9.5 Counting Subsets of a Set: Combinations

    Week 7: Mon Feb 25 - Fri Mar 1

    • Day #17: Section 9.6 r -Combinations with Repetition Allowed (Quiz 5)
    • Day #18: Section 9.7 Pascal's Formula and the Binomial Theorem
    • Day #19: In-Class Exam 2 on Chapter 9

    Week 8: Mon Mar 4 - Fri Mar 8

    Week 9: Mon Mar 11 - Fri Mar 15 is Spring Break: No Class

    Week 10: Mon Mar 18 - Fri Mar 21

    Week 11: Mon Mar 25 - Fri Mar 29

    Week 12: Mon Apr 1 - Fri Apr 5

    Week 13: Mon Apr 8 - Fri Apr 12

    Week 14: Mon Apr 15 - Fri Apr 19

    • Day #35: Supplemental Reading on the Maximum Flow Problem The Maximum Flow Problem an the Augmenting Path Algorithm ( Max Flow / Min Cut Example ) ( Max Flow / Min Cut Example Solutions )
    • Day #36: In-Class Exam 4

      Exam 4 will be five problems, 25 points each:

      1. A problem similar to one of these Textbook Exercises from Section 5.3 involving inequalities: 5.3 # 16, 17, 19, 20, 23
      2. A problem similar to one of these Textbook Exercises involving Big Oh , Big Omega , Big Theta Notation: 11.2 # 4,7,9,17
      3. A problem similar to the Homework Problem on Running Times .
      4. A problem similar to one of these Section 11.3 Exercises about counting the number of basic operations for a simple algorithm: 11.3 # 6,7,8,9
      5. A problem similar to one of these Exercises about showing the result of each step of either the Insertion Sort Algorithm or the Binary Search Algorithm :
        • Exercises about the Insertion Sort Algorithm :
          • Book Exercises 11.3 # 20, 21, 22, 23, 24, 25
          • Supplemental Exercises: Apply the Insertion Sort Algorithm to the following arrays, and construct a table showing the result of each step:
            1. 12, 34, 5, 9, 20, 11
            2. Mark, Rebecca, Nick, Megan, Jennifer, David, Mike
        • Exercises about the Binary Search Algorithm :
          • Book Exercises 11.5 # 5, 6
    • Day #37: Supplemental Reading on Maximum Flow and Minimum Cuts Maximum Flow and Minimum Cuts ( Max Flow / Min Cut Example ) ( Max Flow / Min Cut Example Solutions )

    Week 15: Mon Apr 22 - Fri Apr 26

    Week 16 (Finals Week): Mon Apr 29 - Fri Mar 3

    • Day #41: Mon Apr 29 Final Exam 10:10am - 12:10pm in Morton 122

      Final Exam will be ten problems, 25 points each:

      1. A problem similar to one of these Textbook Exercises from Section 4.1, 4.3, 4.4:
        • Section 4.1 Exercises # 13, 27, 29, 31, 43, 45, 50
        • Section 4.3 Exercises # 2, 3, 4, 12, 15, 16, 19, 24, 26, 27, 28, 29, 30
        • Section 4.4 Exercises # 1, 5, 7, 23, 29, 38
      2. A problem similar to one of these Textbook Exercises from Section 5.1: Section 5.1 Exercises # 3, 5, 12, 14, 20, 46, 66
      3. A problem similar to one of these Textbook Exercises from Section 5.2, 5.3:
        • Section 5.2 Exercises # 6, 8, 10, 13, 20, 22, 25, 28
        • Section 5.3 Exercises # 8, 9, 10, 11, 12, 13, 14
      4. A problem similar to one of these Textbook Exercises from Section 5.6, 5.7:
        • Section 5.6 Exercises # 3, 7, 24, 25, 26
        • Section 5.7 Exercises # 3, 5, 18, 30
      5. A problem similar to one of these Textbook Exercises from Section 9.1, 9.2, 9.3:
        • Section 9.1 Exercises # 2, , 8, 9, 10, 11, 12
        • Section 9.2 Exercises # 1, 3, 4, 6, 10, 11, 14, 26, 27, 28
        • Section 9.3 Exercises # 1, 5, 6, 11, 13, 31, 32
      6. A problem similar to one of these Textbook Exercises from Section 9.5, 9.6, 9.7:
        • Section 9.5 Exercises # 6, 7, 10, 11, 16
        • Section 9.6 Exercises # 1, 3, 8, 9, 10
        • Section 9.7 Exercises # 19, 21, 23, 33
      7. A problem similar to one of these Textbook Exercises from Section 10.1, 10.2, 10.5:
        • Section 10.1 Exercises # 17, 18, 19, 20, 21, 22, 23, 24, 25, 27, 28, 45
        • Section 10.2 Exercises # 12, 17, 18, 23, 25
        • Section 10.5 Exercises # 3, 8, 9, 10, 11, 12, 22, 26
      8. A problem similar to one of these Exercises about Spanning Trees and Shortest Paths:
        • Section 10.7 Exercises # 5, 6, 7, 8, 11
      9. A problem similar to one of these Exercises about Graph Coloring:
      10. A problem similar to one of these Exercises about Counting Basic Operations in Algorithms:
        • Section 11.3 Exercises # 6, 7, 8, 9, 14

    Grading:

    Grading for 2018 - 2019 Spring Semester MATH 3050 Section 101 taught by Mark Barsamian

    During the semester, you will accumulate a Points Total of up to 1000 possible points .

    • Quizzes: 10 quizzes @ 25 points each = 250 points possible
    • In-Class Exams: 4 exams @ 125 points each = 500 points possible
    • Final Exam: 250 points possible

    At the end of the semester, your Points Total will be converted into your Course Letter Grade .

    • A grade of A, A- means that you mastered all concepts, with no significant gaps.
      • 910 - 1000 points = 91% - 100% = A
      • 880 - 909 points = 88% - 90.9% = A-
    • A grade of B+, B, B- means that you mastered all essential concepts and many advanced concepts, but have some significant gaps.
      • 850 - 879 points = 85% - 87.9% = B+
      • 790 - 849 points = 79% - 84.9% = B
      • 760 - 789 points = 76% - 78.9% = B-
    • A grade of C+, C, C- means that you mastered most essential concepts and some advanced concepts, but have many significant gaps..
      • 730 - 759 points = 73% - 75.9% = C+
      • 670 - 729 points = 67% - 72.9% = C
      • 640 - 669 points = 64% - 66.9% = C-
    • A grade of D+, D, D- means that you mastered some essential concepts.
      • 610 - 639 points = 61% - 63.9% = D+
      • 550 - 609 points = 55% - 60.9% = D
      • 520 - 449 points = 52% - 44.9% = D-
    • A grade of F means that you did not master essential concepts.
      • 0 - 519 points = 0% - 51.9% = F

    There is no curve.

    Course Structure:

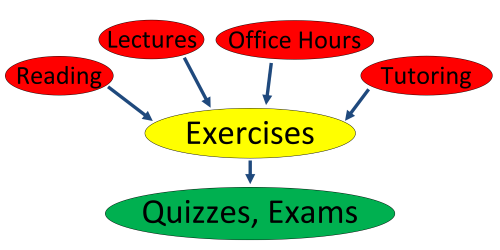
    Course Structure for 2018 - 2019 Spring Semester MATH 3050 Section 101 taught by Mark Barsamian

    One learns math primarily by trying to solve problems. This course is designed to provide structure for you as you learn to solve problems, and to test how well you have learned to solve them. This structure is provided in the following ways.

    • Exercises: These exercises are not to be turned in and are not graded, but you should do as many of them as possible and keep your solutions in a notebook for study.
    • Textbook Readings: To succeed in the course, you will need to read the textbook. The keys to solving the exercises are found in the textbook readings. Some material for the course will be presented in the textbook and not discussed in class.
    • Lectures: In lecture, I will sometimes highlight textbook material that is particularly important, sometimes present material in a manner different from the presentation in the book, and sometimes solve sample problems. We have 37 lectures, totaling 2035 minutes. It is not possible to cover the entire content of the course in 2035 minutes, and the lectures are not meant to do that. (Again, some material for the course will be presented in the textbook and not discussed in class .) Lectures are meant to be a supplement to your reading the textbook and solving problems.
    • Office Hours: Come to my office hours for help on your Presentation Assignments and Exercises! My regular office hours are Mon - Fri from 9am - 10am in my office, Morton 538.
    • Tutoring: Free tutoring is available in the Morton Math Tutoring Lab, in the Math Library, Morton 415a. Make use of it! For information about the Math Tutoring Lab and about other kinds of Tutoring, go to the following link: Student Resources
    • Quizzes, and Exams: Quiz and Exam problems will be based on Lectures, Textbook Readings, and Exercises.
      • Quizzes: There are ten Quizzes. These are roughly 10-15 minutes long and are given at the end of class on the dates shown in the calendar above.
      • In-Class Exams: There are four In-Class Exams. These take an entire class period and are given on the dates shown in the calendar above. The amount of content on an In-Class Exam is roughly four times the amount of content on a Quiz.
      • Final Exam: The final exam is given on the date shown in the calendar above. The amount of content on the Final Exam is roughly twice the amount of content on an In-Class Exam.

    Exercises:

    Exercises for 2018 - 2019 Spring Semester MATH 3050 Section 101 taught by Mark Barsamian

    These exercises are not to be turned in and are not graded, but you should write down solutions for as many of them as possible and keep your solutions in a notebook for study.

    Section 4.1 Exercises # 13, 27, 29, 31, 33, 43, 45, 50, 58

    Section 4.3 Exercises # 2, 3, 4, 8, 12, 15, 16, 19, 20, 24, 26, 27, 28, 29, 30

    Section 4.4 Exercises # 1, 5, 7, 13, 14, 17, 23, 28a, 29, 30, 36, 38

    Section 5.1 Exercises # 3, 5, 12, 14, 20, 27, 46, 53, 59, 66, 81, 83

    Section 5.2 Exercises # 1, 6, 8, 10, 13, 20, 22, 25, 28, 32

    Section 5.3 Exercises # 8-14, 16, 19, 23

    Section 5.4 Exercises # 2, 4, 7

    Section 5.6 Exercises # 3, 7, 24, 25, 26, 37ab

    Section 5.7 Exercises # 3, 5, 18, 19, 24, 26abde, 30, 52

    Section 9.1 Exercises # 2, 7-13, 21, 23, 26, 28, 31

    Section 9.2 Exercises # 1, 3, 4, 6, 10, 11, 14, 16, 17(a,b,c), 18, 26-28

    Section 9.3 Exercises # 1, 5, 6, 11, 13, 31, 32, 33, 35

    Section 9.5 Exercises # 3, 5-7, 10, 11, 13, 15, 16, 17

    Section 9.6 Exercises # 1, 3, 8-10, 16

    Section 9.7 Exercises # 19, 21, 23, 33, 36, 37

    Section 10.1 Exercises # 3, 11, 12, 13, 18, 27, 28, 45

    Section 10.2 Exercises # 1, 4, 5, 12, 17, 18, 23, 25

    Section 10.5 Exercises # 3, 8, 9, 10, 11, 12, 22, 26

    Section 10.7 Exercises # 5, 6, 7, 8, 11

    Supplemental Reading on Coloring

    Section 5.3

    Section 11.2

    Section 11.3 and Handout on Two Algorithms Section 11.3 Exercises # 6,7,8,9,14,20,21,22,23,24,25

    Section 11.4

    • Book Exercises Section 11.4 # 13, 18, 19, 20
    • For the number n = 57, answer the following questions:
      1. Use the formula developed in Example 11.4.3 to predict how many binary digits will be needed to represent n . (Show details of the calculation of the predicted number.)
      2. Express n as a sum of the form \( n = 2^{k} + c_{k-1}2^{k-1} + ... + c_{2}2^{2} + c_{1}2+c_{0} \)
      3. Express n in binary. That is, convert n from base 10 to base 2.
      4. How does your prediction from (a) compare to what you found in (c)?
    • Same questions for the number n = 116

    Section 11.3 and Section 11.5 and Handout on Two Algorithms

    • Book Exercises:
      • Section 11.3 # 20, 21, 22, 23, 24, 25 involving the Insertion Sort Algorithm
      • Section 11.5 # 5, 6 involving the Binary Search Algorithm
    • Supplemental Exercises: Apply the Insertion Sort Algorithm to the following arrays, and construct a table showing the result of each step:
      1. 12, 34, 5, 9, 20, 11
      2. Mark, Rebecca, Nick, Megan, Jennifer, David,Mike

    Supplemental Reading on the Maximum Flow Problem Exercises [1], [2], [3]

    Solutions to selected textbook problems

    Attendance Policy:

    Attendance Policy for 2018 - 2019 Spring Semester MATH 3050 Section 101 taught by Mark Barsamian

    Attendance is required for all lectures and exams, and will be recorded.

    Missing Class: If you miss a class for any reason, it is your responsibility to copy someone�s notes and study them. I will not use office hours to teach topics discussed in class to students who were absent.

    Missing a Quiz or Exam Because of Illness: If you are too sick to take a quiz or exam, then you must

    1. send me an e-mail before the quiz/exam, telling me that you are going to miss it because of illness, then
    2. then go to the Hudson Student Health Center.
    3. Later, you will need to bring me documentation from Hudson showing that you were treated there.
    Without those three things, you will not be given a make-up.

    Missing Quizzes or Exams Because of University Activity: If you have a University Activity that conflicts with one of our quizzes or exams, you must contact me before the quiz or exam to discuss arrangements for a make-up. I will need to see documentation of your activity. If you miss a quiz or an exam because of a University Activity without notifying me in advance, you will not be given a make-up.

    Missing Quizzes or Exams Because of Personal Travel Plans: Many of our Quizzes and Exams are on Fridays. Please don't bother asking me if you can make up a quiz or exam, or take it early, because your ride home is leaving earlier in the day, or because you already bought a plane ticket with an early departure time in order to lengthen your weekend or your Summer Break. The answer is, No you may not have a make-up or take the quiz or exam early. You will just have to change your travel plans or forfeit that quiz or exam.

    Policy on Cheating:

    Policy on Cheating for 2018 - 2019 Spring Semester MATH 3050 Section 101 taught by Mark Barsamian

    If cheat on a quiz or exam, you will receive a zero on that quiz or exam and I will submit a report to the Office of Community Standards and Student Responsibility (OCSSR).

    If you cheat on another quiz or exam, you will receive a grade of F in the course and I will again submit a report to the OCSSR.

    page maintained by Mark Barsamian , last updated April 25, 2019

    View Site in Mobile | Classic
    Share by: