Notes on Modern Physics and Ionizing Radiation

E. Alpha and beta decay

Nuclear substructure by alphas

There are several useful models of the interior of atomic nuclei. Depending on the question at hand, one or another may be more useful in making simple predictions. In many ways the nucleus does act as if it were a liquid drop with attractive interactions between nearest neighbor nucleons when they "touch," but then repulsion if they are forced too closely together (an incompressible fluid). This model of the nucleus was used by Niels Bohr to explain nuclear fission. In other cases a shell model is useful. There are yet other situations in which it is clearly appropriate to visualize the protons and neutrons within nuclei as distinctly correlated, with transient "clumps" of two neutrons joined with two protons: alpha particles. One of the strongest bases for this belief is that many heavy nuclei decay by the emission of alpha particles. Another basis is the otherwise anomalously strong binding of nuclei which could be thought of as being composed of integer numbers of alpha particles, e.g., He-4, C-12, and O-16, as visible in Fig. 1(b) . Still another basis is the outcome when protons of energy a few hundred keV are used to bombard light nuclei: when the target is Li-7, the reaction products are two alpha particles of energy approximately 8 MeV each; when the target is B-11, the reaction products are three alpha particles of similar high energy; and when the target is F-19, the reaction produces one alpha particle and an O-16 nucleus.




Q. M. Tunneling

As predicted by Louis de Broglie, the wave aspect of particles involves a wavelength inversely proportional to the particle's momentum. This approach is valid even in modern quantum theory for those particles whose kinetic energy is positive (the usual case!). For those particles, the probability density of finding the particle in a particular location is the square of the absolute value of a "wave function" that is a complex function of position throughout space. For the simple case that the particle is in a state of motion traveling in a specific direction with a specific momentum, p, and energy, E, that wave function is as shown in Eq. 2a.

whereis a real number, i is as usual the square root of -1, k is the wavevector =/, the +x-axis is in the direction of travel, andis the angular frequency =f. Feynman (1965) presents an interesting derivation of Eq. 2 from relativistic principles. The space dependance reduces to the single complex exponential of Eq. 2b,

The values of k andare related to the macroscopic properties of momentum and energy very simply:

where h is Planck's constant from the theories of the Blackbody spectrum and Photoelectric Effect. (The quantity h/is often written as an h with a "/" through it and spoken as "h-bar.") The photoelectric effect is discussed in Chapter IV because it is the primary mechanism for delivery of energy by a wide range of wavelengths of ionizing electromagnetic radiation. In Chapter VIII we discuss the relationship between wavelength and resolution for microscopes; Eqs. 3 and 4, above, indicate that achievable resolution may be limited by the damagedone by the radiation, because resolution improves with shorter wavelengths, which carry higher energy.

If we take the simple but enlightening case that the state energy, E, consists of kinetic and potential energies, then we can write

where, as usual, U is the potential energy. Hence the wavevector, k, must be related to the potential energy and state energy according to Eq. 6:

The consequences of Eq. 6 are more profound than may at first appear. If we substitute into Eq. 2b, we find that

The wavefunction of Eq. 7 has constant amplitude,, throughout space wherever the state energy exceeds the potential energy. This is in accord with the Heisenberg Uncertainty Principle, which asserts that any state that involves an exact momentum cannot be localized to a specific region of space! Furthermore, Eq. 7 indicates behavior that is clearly sensible to regard as a traveling wave when we include the time-dependance from Eq. 2a.

We will now try to extend Eq. 7 beyond the realm for which it has been derived: we consider what it might mean in places where the potential energy exceeds the state energy. Where would those places be? By inspection of Eq. 5, we see that they are regions where the kinetic energy would be negative, hence they are classically forbidden regions: classical physics asserts that the object will neverbe found in those places. An example would be the top of a hill up which a ball is rolled from the bottom with too slow a speed to reach the top (i.e., at the bottom the kinetic energy it has is less than the gravitational potential energy it must gain to reach the top).

The mathematics of Eq. 7 makes a simple and interesting assertion about the wavefunction, and hence the probability of finding the object, in those forbidden regions. Where E < U, the radical in the exponent will contain a negative number, hence it will be pure imaginary. The product with i is then a negative real number and we find the following:

This says that as we proceed (in the direction the object was headed) into the classically forbidden region, the probability of finding the object does notplunge suddenly to zero, but rather falls off gradually according to the negative exponential of Eq. 8. If the potential energy function U(x) has a region of finite thickness in the direction of travel throughout which it exceeds the state energy, E, then the wavefunction will nothave fallen to zero at the far side, and hence the wavefunction will include travelling waves on bothsides of the barrier. This mechanism is usually described as "quantum mechanical tunneling," the object has gone "through" the barrier, not "over" it.




a.  Alpha Decay

There are three specific applications of quantum mechanical tunneling that we will discuss here. The first is alpha decay of radioactive nuclei. This approach to understanding alpha decay was originated in 1928 by E. U. Condon and R. Gurney at Princeton, and independently by the Russian, G. Gamow, then working in Germany (see Olsson, 1992 , and Cathcart, 2004 ). The potential energy function for alpha particles near or within nuclei can reasonably be approximated as shown in Fig. 4(a), where the zero of potential energy is taken at infinite separation from the nucleus. The alpha particle interacts with the rest of the nucleus in two ways: they repel each other according to Coulomb's Law of electrostatic forces, and they attract each other by the nuclear strong force whenever the separation is less than about 1 fm. The net effect of the various forces is that the alpha particle is free to move around the interior of the nucleus, that it experiences a very strong attractive force when at the nuclear boundary ("surface tension"), and that it experiences a very strong repulsive force when beyond the nuclear boundary by more than about 2 fm.



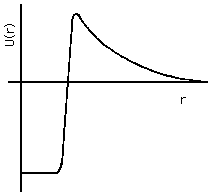
Figure 4a: Alpha-particle Potential Energy in and near Nucleus.


In the case of stable nuclei, the alpha particle's state energy is less than zero, so that the wavefunction outside the nucleus is a negative real exponential all the way out to infinity, and the only significantly likely place to find it is within or just outside the nucleus itself. In the case of radioactive nuclei, the state energy is positive, but not as positive as the peak value of U(x). Thus the wavefunction for the alpha particle will be large inside the nucleus, but notzero in the space distant from the nucleus. The relative proportion of the wavefunction inside and beyond the nuclues relates directly to the mean lifetime for alpha decay: the closer the state energy approaches to the peak value of U(x), the more probable it is to find the alpha particle outside and the shorter the mean life.




b.  Field Emission

The second application is field emission. Qualitatively, this can be described as the ripping of valence electrons from the interior of a piece of metal by the application of strong electric fields. It is the method by which the highest resolution electron microscopes create their working beam of electrons [ Crewe, 1971 ]. As discussed in chapter IV, the potential energy for an electron within or near to a conductor's surface can be approximated simply as a step function, with one value in the interior and a higher value in the exterior region. The difference between the two values is essentially the binding energy of the valence electrons.

If another conductor is placed nearby and a large potential difference applied between the two, the potential energy of the electron will be lower at the positively charged electrode (the anode) and higher at the negatively charged one (the cathode); see Fig. 4(b) and Figs. IV-2 and IV-3 . Thus, throughout the region of space between them, the potential energy must slope, and near the surface of the cathode U(x) will reach a peak value and decline. The cathode valence electrons have a state energy typically 1 to 3 eV below that peak, so if the potential difference between cathode and anode is large enough, and their separation in space is small enough, the barrier will be so thin that there will be a usefully large probability for those valence electrons to tunnel out of the cathode and be accelerated away to the anode.



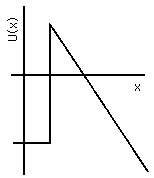
Figure 4b: Electron Potential Energy in and near Cathode.


The advantages of the field emission for electron microscopy are that the electrons are cold, hence they have a very small random component to their velocities. This means that they will follow very predictable trajectories through the instrument, and hence can be brought to a very sharp focus, probing a tiny area of the sample. The slope of U(x) must be quite steep, however, in order to produce a "thin" enough barrier to permit a significant probability of penetration. This cannot be achieved just by using a large potential difference with two electrodes that are held parallel to each other a small distance apart: the insulation on their mechanical supports would break down. Instead, what is done is to use a cathode that is a rod brought to a very sharp point. The electric field concentrates at such a point, since it must be everywhere perpendicular to the surface of a conductor. Predictability of the trajectory then requires that the tip of the point be shaped very smoothly into a hemispherical dome; surface tension of a molten metal suffices to hold a good spherical shape, but since the tip is made of atoms there is a limit to the smoothness that can be achieved! These points, among others, are discussed in detail by Crewe.




c.  Nuclear Bombardment

The third application is the impact of low energy nucleons or alpha particles onto nuclei. There are two possible outcomes:

• an elastic collisionproduced in essence by the Coulomb repulsion, although perhaps modified in detail by the nuclear interaction for higher energies (in which the bombarding particle has enough kinetic energy to penetrate close to the nuclear surface, and therefore be within range of the strong nuclear force), and
• a nuclear reactionif the Coulomb barrier is surmounted or penetrated.

George Gamow was the first to apply tunneling theory to the problem of reverse radioactive decay: when a positive projectile (such as an alpha particle or proton) is used to bombard a nucleus, it need not have enough initial kinetic energy to exceed the maximum height of the Coulomb barrier in order to have a non-zero probability of penetrating into the interior of the nucleus, thus initiating a nuclear reaction (see Cathcart, 2004 ).

Because the probability of penetration is the negative exponential of the height of the barrier above the state energy times the thickness, the reaction probability (rate) will depend very stronglyon bombardment energy.

As discussed later, stellar nucleosynthesis is the mechanism by which elements other than hydrogen are formed. Our understanding of stellar interiors is based in part on the observed abundances of the various elements, combined with experimental nuclear physics data resulting from the bombardment (in "atom-smasher" accelerators) of various nuclei with protons, neutrons, alpha particles, etc. Because the lab data must be taken at high enough energies (typically around 1.4 MeV, except for the lightest target nuclei) to observe a statistically significant number of reactions in a reasonable period of time, elaborate calculations are required to extrapolate the measured rates to the rates that should be expected in the interiors of stars, where the thermal energies are typically around 0.3 MeV. This places a great premium on experimental persistence, including tightly controlling the energy at which the data are obtained.




Alpha Decay Energy

Alpha decay is a change from the ground state of an original nucleus to an excited or ground state of a daughter nucleus with the expulsion of an alpha particle. The energy released in this change will be shared as kinetic energy by the alpha particle and the recoiling daughter nucleus. Since the total momentum is initially zero, the alpha particle and the daughter nuclues must move in exactly opposite directions with the same magnitude of momentum. Thus the fixed total kinetic energy will always be split between the alpha and the daughter nuclues in the same way, depending on the mass of each. The spectrum of kinetic energies of the alpha particles immediately after decay will be as shown in Fig. 5.



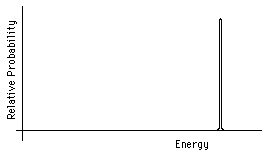
Figure 5: Alpha particle energy spectrum.




Beta Decay Energy

Beta decay presents a significantly different situation: there are three final objects, the daughter nucleus, the electron or positron, and the neutrino or antineutrino (see the next session for a further discussion of neutrinos). Thus, conservation of momentum and of energy do notsuffice to determine the kinetic energy given to the beta particle, there are too many unknowns. We must therefore expect a spectrum of initial beta kinetic energies to be as shown in Fig. 6 (after Marmier and Sheldon, 1969, Fig. 8-4 ; see also Cember, Fig. 4.4, page 70 , or Ford, Fig. 26.6(b), page 1326 ).



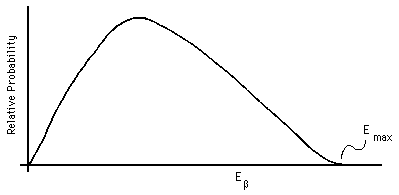
Figure 6: Beta particle energy spectrum.


Conservation of momentum and energy do allow us to state that there will be a definite maximum kinetic energy given to the beta particle, occurring in the limit as the momentum and energy given to the neutrino approach zero. In this case the momentum and energy of only two particles need to be taken into account, giving us the same algebra as alpha decay.

Measurements of the exact shape of the beta particle energy spectrum can be used to calculate an upper limit on the value of the neutrino's mass. At this time the uncertainties in measurement are so large that a zero mass appears possible, and a tiny mass certain. As discussed in the next section, other evidence points convincingly to a small, but non-zero, mass.




Electrons, Muons, and Neutrinos

Muons are elementary particles very like electrons (they carry one unit of electrical charge, appear to have zero radius, have spin one-half, etc.). However, unlike electrons, they are not stable, but rather decay (usually within a few microseconds), their mass is 206.768 times an electron's mass, and there are separate conservation laws for muon number and for electron number. The electron and the muon each have associated with them a neutrino and its anti-neutrino; neutrinos have zeroelectric charge and nearly zero rest mass: they have been observed to exist only in motion, carrying kinetic energy at nearly the speed of light. The electron number is calculated as the number of electrons present plus the number of electron neutrinos, minus the number of anti-electrons (positrons), minus the number of electron anti-neutrinos. The muon number is calculated, in analogy with electrons and positrons, by counting as positive the negatively-charged muons and the muon neutrinos and counting as negative the positively-charged muons and the muon anti-neutrinos.

As of the fall of 2012, research indicates that the neutrino's mass cannot actually be zero. The neutrino's mass appears to be between 1 eV and 1 meV (that is millielectronvolt, notMegaelectronvolt), less than 0.0002% of the mass of the electron. As a result of the big bang at the beginning of the universe, there are presently several hundred neutrinos per cubic centimeter throughout the universe. Wolfenstein, 1987 , presents a nice summary of neutrino physics in his review of Fackler and Vân, 1986 .

In all reactions and decays, including the decay of the free muon, both electron number and muon number are conserved. Thus the two muons will decay according to the following schemes:

Donelly and Jensen (1964) and Frisch and Smith (1963) measured the relativistic time dilation of the lifetime of fast-moving muons. In a simpler experiment, we can measure the lifetime of muons at rest with respect to our laboratory equipment. Muons can be produced in a variety of ways; they are produced naturally at the top of the atmosphere following collisions of high energy cosmic rays with the atmosphere, primarily oxygen or nitrogen nuclei. The muons shoot toward the surface of the earth at speeds greater than 99% of the speed of light. Many of them disintegrate in flight on the way down, but some survive the trip through the atmosphere and eventually decay after being stopped in the earth or in matter near the surface of the earth, such as our lab equipment.

When a muon decays, the reduction in rest mass present will be compensated by an increase in kinetic energy, in order that the total mass-energy stay constant. This kinetic energy is shared between the electron (or positron) and the two neutrinos, in proportions that vary widely. We have already seen a typical distribution of electron kinetic energy in such beta decays. Most of the electrons from muon decay will be moving well over half the speed of light.

As is usual in beta decay, that part of the energy carried away by the neutrinos is not detected, but the kinetic energy of the decay electron (or positron) can be. In the case of a positive muon, which decays into a positron, there will be additional energy available for detection, because the positron will annihilate with an electron from the matter where it stops. This produces two photons of energy 0.511 MeV, as discussed in chapter IV.

One version of the experiment studies the decays of muons that stop in a cylindrical plastic scintillator of approximately 7 liters volume. This plastic is compounded to be particularly efficient at converting the kinetic energy of fast charged particles into visible light photons. Cosmic ray muons that reach the surface of the Earth are moving very fast, so those that stop in the plastic have enough kinetic energy to produce a great many visible light photons.

We need only to measure the time between the flash of visible light generated by the scintillator when the muon stops and the later flash of light generated when the decay beta particle stops, in order to determine the lifetime of that particular muon. By measuring the lifetimes of many muons, we can determine the average lifetime. The calculation is of course complicated by the fact that we do not see every muon decay; some by chance will live longer than the time visible to our apparatus, and some will decay so quickly that the two flashes of light will seem as one.

A photomultiplier tube converts the light flashes into sudden bursts of electrical current. The electrical signal travels onward to electronic amplifiers that convert the current bursts into voltage pulses that can be examined quantitatively. The amplifiers include circuitry to remove as much as possible of the random noise while still producing output pulses sharp enough to permit precise statement of the time at which they occur. The amplified signals may be examined on an oscilliscope or with an "interval timer" circuit that records the time interval between pulses. Many of the observed pulses will be other types of events than muons stopping and decaying, but most of the others will occur with much longer or much shorter intervals before the next pulse and after the previous pulse, so that an accurate determination of the muon lifetime is still possible.




Other Beta Decay Mechanisms

For radioactive decay to occur spontaneously, the final state of the matter must have a lower energy than the initial state. The accounting must include the atomic electrons, the decay particle (alpha or beta), and the mother and daughter nuclei. In some cases the daughter nucleus has a lower energy than the mother nucleus, but not by enoughfor ordinary beta decay, because of the 0.511 MeV of energy required to create the beta particle's mass, as calculated from Eq. 1.

If the obstructed beta decay would have been positron emission, there is another path that may, and in some cases does occur: capture by the nucleus of an orbital electron. This is essentially a reverse negative beta decay, instead of emitting an electron, one is absorbed. The nucleardecay then proceeds as shown in Eq. 10,

where we have identified the nuclei by their numbers of neutrons and protons and where the electron on the left side is the atomic electron, already in existence. As in all beta decays, the electron number will be conserved by the emission of an appropriate neutrino.

After the nucleus has captured the electron, we are left with a daughter nucleus of charge +(Z-1)e that is surrounded by (Z-1) electrons, hence still a neutral atom. However, the electrons most likely to be captured are those whose wavefunctions gave them the largest probability of being close to the nucleus: the inner-shell electrons. Therefore, it is extremely unlikely that the daughter atom will find its electron structure in its ground state. It will instead typically be in a highly excited state, often one in which the innermost shell has one vacancy and the outermost shell is slightly excited also. The result is simply that the electron structure relaxes promptly to its ground state, emitting one or more photons. Since the electrons are at that time surrounding the daughter nucleus, the photon energies will be characteristicof the daughterspecies. Because these photons are emitted by relaxation of atomic electron excitation, they are called "X-rays."

Another obscure form of beta decay that is seen involves the interaction of the beta particle with the nucleus or atomic electrons "on the way out," giving rise to secondary radiation that can be observed at a distance. This "internal conversion" does not produce monoenergetic photons, because there is still the initial partition of the decay energy between the daughter nucleus, the beta particle, and the neutrino.




Decay Chains

It will frequently be the case that the daughter nucleus of a radioactive decay is itself radioactive and undergoes further decay. For the very heavy elements, near and beyond uranium, the typical situation is to have a long sequence of such decays, some with very short half-lives, some with much longer lifetimes.

The phrase "secular equilibrium" is used to describe a mixture of isotopes such that all of the "daughter" species are being created by decay just as rapidly as they are decaying.

The resulting daughter nuclei, in their turns, will decay also, ending finally with the one stable terminus of that decay chain. All of the trans-Uranic decay chains terminate with a stable isotope of lead or of bismuth; as discussed earlier, no element beyond bismuth (Z = 83) has anystable isotope.

Because beta decay, which changes a neutron into a proton, leaves the atomic mass number A (which is equal to N+Z) unchanged, and alpha decay reduces A by 4, there are four distinct heavy-atom chains, known as the 4n, 4n+1, 4n+2, and 4n+3 chains. Figure 8 shows a modified version of the upper right corner of Fig. 2. Each of the four heavy-element decay chains is shown in a different color:

• The natural 4n chain is shown in green and starts with Pu-240.
• The artificial 4n+1 chain is shown in yellow and starts with Am-241.
• The natural 4n+2 chain is shown in blue and starts with U-238.
• The natural 4n+3 chain is shown in red and starts with U-239.







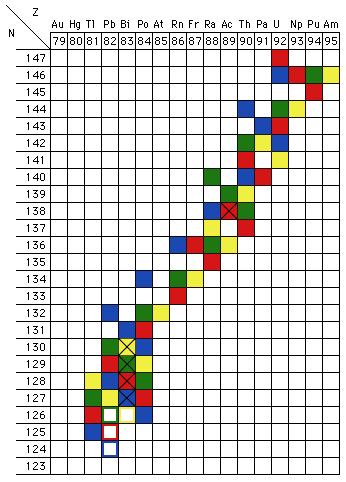
Figure 8:Trans-Uranic decay chains. The data used are those tabulated in the 67th Edition of the CRC Handbook of Chemistry and Physics (the various editions differ on a few decay paths). Isotopes marked "X" exhibit both alpha and beta decay. The hollow blocks are the stable end-points of the decay chains.

---


The heavy element decay chains also illustrate another feature of radioactive decay: some nuclei have twoseparate decay routes, both alpha decay and either positive or negative beta decay. In terms of the chart of the nuclides , Fig. 2, an isotope down in the valley of stability, but not stable, will move to a state of lower energy only by alpha decay. Likewise, an isotope far up on the walls of the valley will move to a state of lower energy most directly by "heading downhill," undergoing beta decay (positive if the isotope is on the Z-axis side of the line of greatest stability, negative if it is on the N-axis side, which is typically the case for all of the trans-Uranic decay chain illustrated in Fig. 8). If, however, the isotope is only a little way up from the bottom of the valley, alpha decay may be about as likely as beta decay. In those cases, then, both decays will be observed, in some proportions. The isotopes that undergo both alpha and beta decay are shown in Fig. 8 with a black "X" in their cell of the chart. (The viewpoint described in this paragraph is inspired by my memory of a presentation made by one of its members to the Michigan Section of the AAPT in the late 1970s or early 1980s; I have not been able to establish who or when.)

In principle, reasoning soley on grounds of energy conservation, it might be the case that an odd Z, odd N nucleus could decay threeways: by alpha, negative-beta andeither positive-beta or electron capture. Both beta decays would produce even Z, even N daughters, which might both be so tightly bound that their formation would be exothermic. I do not know if a sample of any isotope has ever actually been observed to decay all three ways.

As you can see in Fig. 8, allof the naturally occurring heavy element decay chains include at least one isotope of radon (Z = 86), which is a gas at room temperature. This can be a major health hazard in two ways:

1. The chemically inert radon gas can be inhaled and circulated throughout the body, where it has some probablility of decaying.
2. The decay products of radon are radioactive heavy metals; since the radon atom was free-floating, the result is to create radioactive monatomic heavy metal dust, which can penetrate all the way into the lungs; this may pose chemical as well as radioactive hazards.

The radon accumulated inside a building can achieve significant concentrations; these issues are not just hypothetical concerns. The problem is compounded, of course, for those houses built upon fill rock that was uranium mine tailings!

Hubbard (1989) comments that "... the major source [of indoor radon is]: flow into the indoor air of radon-containing soil gas, driven by pressure differences between the soil gas and the indoors." The pressure differences required are tiny: 0.01% of an atmosphere is enough to change the air once per hour in a typical house. This can be readily provided by the "stack effect" of indoor winter heating. External venting of clothes dryers that take their air from the interior of the house will further reduce the air pressure inside with respect to the soil gas pressure. The concentration of radon in air between soil grains is roughly 10,000 Bq/cubic meter ( Nero, 1989 ), so that even a low rate of diffusion into the house can be significant.

Nero (1989) comments further that the 10's of Bq/cubic meter typical of indoor air causes cancer risk comparable to 2-3 mSv to the entire body (1 millisievert = 0.1 rem; see discussion of radiation dose and exposure measurement in Chapter VI ). The typical health risk from radon is comparable to 10% of that from smoking. Usually basement air exhibits a significantly higher concentration of radon than the upstairs living spaces. Outdoor radon concentrations are typically derived from the top meter of soil. Sandy, gravelly soils result in a ready diffusion of gas through the soil.

Rn-222 is the isotope of radon that presents the primary health hazard, based on its half-life (3.8 days, long enough to diffuse through significant thicknesses of soil, rock, and concrete) and abundance (it is in the chain down from U-238, the most abundant isotope of uranium). To make matters worse, the 5.5 MeV alpha particles emitted by Rn-222 and the 5.2 MeV alphas emitted by Po-218, its first daughter in the decay chain, penetrate about 50 microns in tissue, just reaching from the surface of the mucous layer, where they are deposited, in to the epithelial cell layer that is most rapidly growing in the lining of the lungs' airways ( Socolow, 1987 ; see also Toohey, 1987 ). Abelson (1991) points out that an accurate evaluation of the health hazards of radon is made more difficult by the fact that the primary cases of high level exposures were compounded with exposures to other mineral dusts and to tobacco smoke amongst workers in the uranium mines of the Colorado Plateau during the 1950s.

F. Electron relaxation and X-rays

Immediately after a nuclear decay we will find that what had been a neutral atom of the mother species has become an ionof the daughter species; because the nuclear charge has changed, the number of electrons in orbit about the nucleus no longer matches the number of protons inside the nucleus. This has two consequences: first, the ion will neutralize itself by stealing an available electron from a neighboring atom or by shedding an excess electron. Second, the resulting new neutral atom is likely to be in a highly excited state: the wave functions for the electrons of the mother atom in its ground state have significant probabilities to be ground orexcited states of the daughter nucleus. When, typically quite promptly, the daughter atom's electrons relax into their ground state, the excess energy is radiated away as one or more photons. Since the transition is between states of the daughter atom, the energy spectrum of these X-rays is characteristicof the daughterspecies, notof the mother species. The health hazard from these X-rays is sometimes far more acute than the hazard from the alpha or beta radiation of the nuclear transformation itself.

G.  Nuclear excitations and gamma rays

The second mechanism by which photons are given off following a nuclear transformation is that the daughter nucleus may well be in an excited nuclearstate; the arrangement of protons and neutrons within the volume of the mother nucleus may have a large or small probability to change to the nuclear ground state arrangement of the daughter nucleus. If the daughter nucleus is first created in an excited state, it will, typically quite promptly, undergo a transition to its ground state, emitting one or more photons to carry away the excitation energy. Such photons are known as "gamma rays." Since they occur from transitions between states of the daughter nucleus, they are characteristicof the daughterspecies. Because nuclear excitations are typically high energy, these gamma rays usually are much more energetic than the atomic electron relaxation X-rays discussed above.

Dick Piccard revised this file ( https://people.ohio.edu/piccard/radnotes/alphabeta.html ) on September 18, 2012.

Please E-mail comments or suggestions to piccard@ohio.edu .